こんにちは@hagino3000です。Zucks Ad Networkという広告配信サービスの開発をしています。最近はアドネットワークの広告配信最適化に利用できるアルゴリズムの調査もしています。
本稿では調査で読んだ論文の一つ、オンライン広告配信を想定した多腕バンディット問題である、Mortal Multi-Armed Banditsを紹介します。多腕バンディット問題になじみがある読者を想定しています。
オンライン広告と多腕バンディット問題
ここでは簡単のために、クリック課金型のディスプレイ広告を前提に説明します。オンライン広告配信システムにおける問題として「最初はどの広告がどれだけクリックされるかわからないが、なるべくクリックされる広告を多く配信したい。」という物があります。これは多腕バンディット問題として知られており、探索はCTRが推定できるまで配信する事、活用はeCPMが高い物を配信する事、にあたります。
しかし、腕が無限回数引けるとする標準的な多腕バンディット問題設定に対して、広告配信システムでは広告毎に予算や有効期間があります。予算が無くなれば腕は引けなくなる、その一方で新たな腕も生まれます、これを制約として盛り込んだ物をこの論文では mortal multi-armed bandit problemと呼んでいます。
腕の報酬と死のモデリング
この論文中では腕の報酬モデルを次の2つで定義しています。
- state-aware
- シンプル
- 報酬は固定、一度引けば得られる報酬が判明する
- state-oblivious
- より現実的
- 0もしくは1が腕に設定された確率に基づいてランダムに得られる
腕の死についてのモデルは次の2つ
- budgeted death
- 腕に設定された予算
を越えて引くと死ぬ
- 腕に設定された予算
- timed death
- パラメータ
の幾何分布に従って死ぬ
- 期待生存時間
- パラメータ
state-obliviousケースは、腕毎にCTR相当のパラメータを持つと解釈できます。
提案手法のベースとなるアプローチ
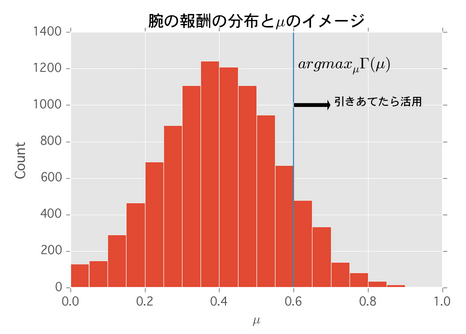
配信実績データから腕の期待生存期間、報酬の分布とその累積分布 を求めておく。 ここから次の式
を最大にする
を求めます。
は腕の期待報酬、
は腕の期待生存期間です。求めた
より高い報酬が得られる腕を引き当てたら、腕が死ぬまで活用
するという決定的なアプローチです。
式に注目すると、腕の生存期間が1、つまり一度しか腕が引けない場合はも
も関係ありません。この場合は戦略の取りようが無いので腕の期待報酬にのみ依存するのがわかります。逆に腕の生存期間を動かしながら
をプロットすると次の通りになります。

腕の期待生存期間が長い程は大きくなります、よって活用する腕の選定が厳しくなります。最もシンプルなstate-awareケースに対する処理をPythonで実装すると次の通りになります。
class DETOPTStateAwareStrategy(object): def __init__(self, p=0.01, arms=100): self.arms = MortalArms(arms, p, aware=True) self.mu = maximize_gamma_mu(1/p) self.current_arm = None def pull(self): self.arms.update() arm = self.current_arm if arm is None or arm.is_live == False: arm = self.arms.select_new_one() reward = arm.pull() if reward > self.mu: self.current_arm = arm # 次回も活用 else: self.current_arm = None # 別の腕を探索 return reward
提案手法と既存手法の比較
state-obliviousケースでの各手法のシミュレーション結果が載っていたので、手元でも実装して比較してみました。この論文の提案手法でパフォーマンスが良い物2つとUCB1を比較してみます。
- STOCH. WITH EARLY STOPPING
- 腕の報酬が推定できるまで連続して引くが、駄目そうなら途中で切り上げる
- 腕の推定報酬 >
であれば腕が死ぬまで活用する
- ADAPTIVE GREEDY heuristic
- Epsilon-Greedyがベース
- 探索率はその時のベストな腕の推定報酬によって変える
- UCB1
- 既存手法
- 腕の推定報酬と引いた数から次に引く腕を決める決定的な手法
STOCH. WITH EARLY STOPPINGは次の通り。
class StochasticWithEarlyStoppingStrategy(object): def __init__(self, p=0.01, arms=100): self.arms = MortalArms(arms, p, aware=False) self.mu = maximize_gamma_mu(1/p) self.current_arm = None self.pulled_count = defaultdict(int) self.reward = defaultdict(int) def pull(self): self.arms.update() arm = self.current_arm if arm is None or arm.is_live == False: arm = self.arms.select_new_one() self.current_arm = arm reward = arm.pull() self.pulled_count[arm.index] += 1 self.reward[arm.index] += reward n = 15 pulled = self.pulled_count[arm.index] if pulled < n: if (n - pulled) < (n*self.mu - self.reward[arm.index]): self.current_arm = None # 次の腕を探索 elif pulled == n: if self.reward[arm.index] <= n*self.mu: self.current_arm = None # 次の腕を探索 else: pass # 死ぬまで活用 return reward
ADAPTIVE GREEDY heuristicは次の通り、パラメータcは人間が経験で決めるそうです。
class AdaptiveGreedyStrategy(object): def __init__(self, p=0.01, arms=100, c=1): self.arms = MortalArms(arms, p, aware=False) self.pulled_count = defaultdict(int) self.reward = defaultdict(int) self.c = c @property def best_arm(self): """ 過去に引いた事がある and まだ生きている腕から推定報酬最大の腕を返す """ mean_rewards = [] candidate_arm_idxs = [] for i in self.reward.keys(): if self.arms.select(i).is_live: n = self.pulled_count[i] r = self.reward[i] candidate_arm_idxs.append(i) mean_rewards.append(r/n) if len(candidate_arm_idxs) == 0: return None best = mean_rewards.index(max(mean_rewards)) if best >= 0: return self.arms.select(candidate_arm_idxs[best]) return None def pull(self): self.arms.update() best_arm = self.best_arm if best_arm: p = self.reward[best_arm.index]/self.pulled_count[best_arm.index] if np.random.random() < min(1, self.c * p): arm = best_arm # 活用 else: arm = self.arms.select_random() # 探索 else: arm = self.arms.select_random() # 探索 reward = arm.pull() self.pulled_count[arm.index] += 1 self.reward[arm.index] += reward return reward
結果
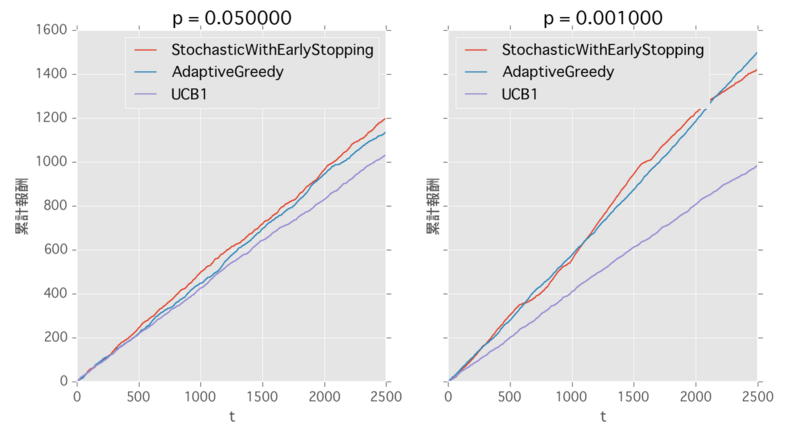
提案手法はUCB1よりも良く、STOCH. WITH EARLY STOPPINGとADAPTIVE GREEDYがほぼ同じパフォーマンスとなりました。論文の実験結果と同じですね。
まとめ
腕の入れ替りを制約に盛り込んだmortal multi-armed bandit problemを紹介して実装してみました。今回の腕のデータはガウス分布で作ったので、より深い検証が必要であれば実データを元にした腕の数や予算にする必要がありそうです。
しかし、良い腕を連続して引き続けるというのは、実際の広告配信の動作イメージとは異なります。また期待報酬が少ないからと言って全く配信しないのも予算消化の観点で問題がありそうです。このあたりは確率的に腕を引く手法に分がありそうです。理論限界や性能の証明については省略したので論文を参照していただければと思います。
省略した物も含めて今回の実験コードはnbviewerにアップしました。
References
Deepayan Chakrabarti, Ravi Kumar, Filip Radlinski, Eli Upfal Mortal Multi-Armed Bandits (NIPS 2008)



