この記事はVOYAGE GROUP Advent Canlendar の14日目の記事です。
皆さまこんにちはこんばんは。 コンテンツメディア事業本部の 坂本 がお送りいたします。
ビリヤード、楽しいですよね。 空間把握能力, 物理的特性の理解, 理想のイメージと身体動作への再現などが試される良質なスポーツだと思います。
そんなわけで（？）、「ビリヤードの物理的特性を活かせば論理回路作れるのでは？」と思いついたので作ってみました。 （最後の方に実際にビリヤード場で撮影した動画もあります！）
基礎知識
この記事では、プレイヤーがキューで撞く（つく）玉を「手球（てだま）」、それ以外の数字が振られた玉を「的球（まとだま）」と呼びます。
手球が的球にスピードを持って接触したとき、的球が進む方向は2つの球の中心を結んだ直線になります。
↑的球が進む方向は2つの球（たま）の中心を結んだ直線になります（大事なことなので2回言いました）。
これを利用すると、狙いが雑でも常に同じ方向に進む球を作ることができます。
↑2つの的球を予め接触させておくと、後ろの的球は常に同じ方向に進みます。
球の進行方向が定まることで、回路の再現性を担保することができます。
導線（NOTNOT回路）
論理回路には入力と出力があります。 ビリヤード台の上で0と1をどのように表現すればよいでしょうか。
最終的な出力はやっぱり「0 = 球がポケットに入らない, 1 = 球がポケットに入る」で表現したいですよね。気持ちがいいですし。 これはすなわち「0 = 球を転がさない, 1 = 球を転がす」ことと同義です。
一方で、入力を「0 = 球を撞かない（転がさない）, 1 = 球を撞く（転がす）」だけとしてしまうと、単純に考えてNOT回路を作ることができません……。 手球を撞かずに的球をポケットに入れるなんて無理ですからね。
そこで「0 = 球を撞かない, 1 = 球を撞く」という入力以外に「回路を実行するショット」を導入します。 （この「電源」とも呼べる発想に至るまで少し悩みました ◜◡◝ ） さらに球の進路を妨害する球を置くことで、「0ならば0, 1ならば1」となる回路（導線）を実現できます。
入力は「妨害の妨害」をしているのでNOTNOT回路と考えてもいいかもしれませんね。
さて、これで準備は完了です。 いよいよお待ちかね、主役級の論理ゲートたちの登場です！
AND回路
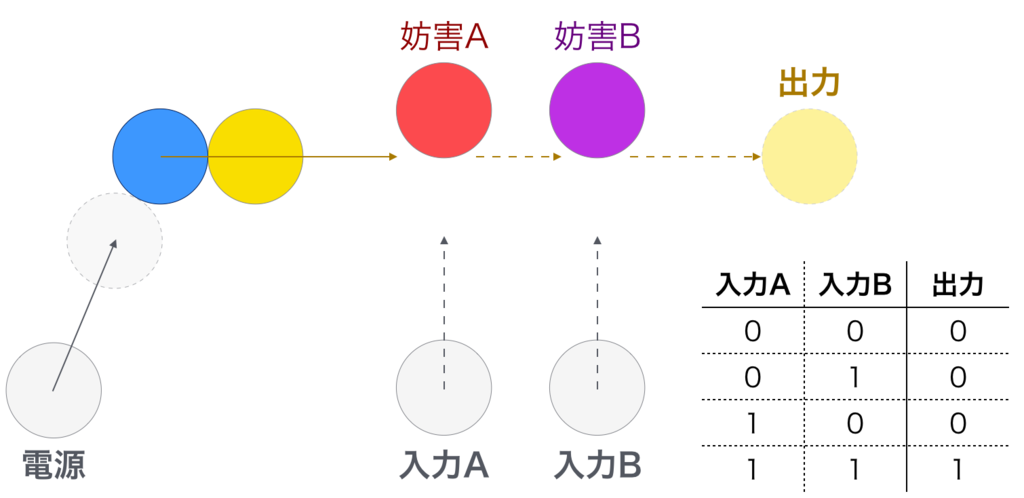
2つの入力それぞれに妨害球を排除する役目を与えることで、「両方の入力があったときだけ球が出力される」= AND回路を実現することに成功しました。 一目瞭然で非常にいい感じです( ◠‿◠ )
この構造の優秀なところは、球が3個以上でも同じ配置を足せばいいだけであることですね。 スケーラビリティがあります。
OR回路
2つの入力をどちらも1つの妨害球を排除する役目を与えることで、「片方または両方の入力があったときだけ球が出力される」= OR回路を実現できます。
これまた球が3個以上でも同じ構造で対処できます。
NOT回路
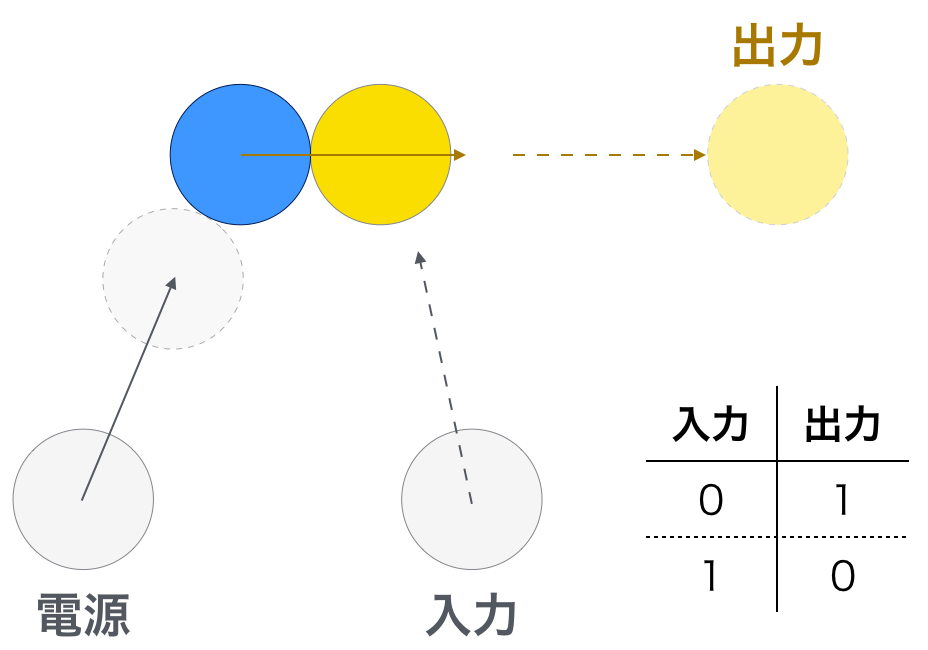
NOT回路では逆に、これまで球の射出に使っていた部分を入力によって破壊します。 これによって、入力がなければ出力があり、入力があれば出力がなくなります。
NOR回路
NAND回路より簡単なのでNOR回路を先に説明します。
NOT回路の入力を並列にすることで、「片方または両方の入力があったときだけ球が出力されない」= NOR回路になります。 これまた球が3個以上でも受け入れられるスケーラブルな構造です。
別パターンとしてNOT回路を直列に繋げる方法もあります（下図）。
NAND回路
急に球が増えましたね。 こちらはNOT回路そのものを並列にすることで、「両方の入力があったときだけ球が出力されない」= NAND回路になります。 最初に球の射出を分岐させて、最後に同じ箇所に集まるようにする仕組みです。
この配置では残念ながら3個以上の球には対応できません。
上の図では大変そうなNAND回路ですが、入力を非対称にする（順序を与える）ことで、かなり簡潔にすることができます。
入力A→入力Bの順に与えたときだけ球が出力されません。 さらに3個以上の球であっても、妨害球を使って入力を直列に繋げることで対応可能です。 入力A, Bと赤い球の部分は、よく見ると最初に紹介した「導線（NOTNOT回路）」の電源を入力とした形になっています。
XOR回路
これまでの組み合わせによって頑張ると、XOR回路を頑張ることができます。
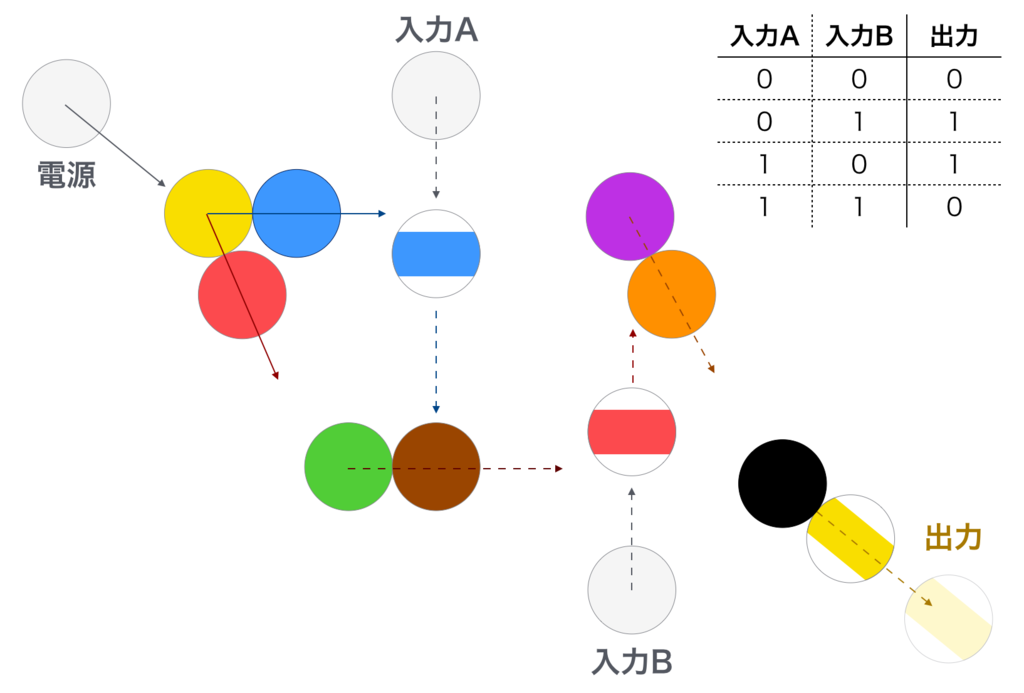
美しい……。 ストライプの球（9番以降）まで登場して所狭しですが、点対称の造形美がありますね。
下図のように考えると若干わかりやすくなるかと思います。
( AかつnotB ) または ( notA かつ B ) ─── そう、実は積和標準系そのものなのです！
上のルートは「AありBなし」のときだけ出力され、下のルートは「AなしBあり」のときだけ出力されます。 そしてその和をとることで最終的に「AかBの片方」のときだけ出力される寸法です。
上図はXOR回路の一例でしかなく、工夫次第で簡略化できる可能性があります。 また、例えば電源をルートごとに複数回にすれるほうが実際の精度は上がるかもしれません。
やってみた
実際のビリヤード場で論理回路を組んだ様子の動画です。
※ 上で紹介した回路の中に、撮影時には思いついてなかったものがあるので収録されていないものがあります。ご了承くださいm(_ _)m
まとめ
ビリヤードたのしい
明日のAdvent Calendarは@akiyahさんです！
