コインを投げを観測し、コインの表になる確率を予測するとき、みなさんはどのように予測するでしょうか。 (コイン投げに限らず、表か裏のように二値になるような予測であれば、例えば、広告のクリック率や、単語の出現率、ナンパの成功率でもなんでもいいです。)
コインが表になる確率が0から1まで一様だ(まんべんなく出る)とすれば、n回投げてs回表を観測したら、平均であるs/nをその確率として予測するのではないでしょうか。
この方法をもっと複雑な言い方をすれば最尤推定(maximum likelihood; ML推定)とよびます。コインが表になる確率が一様という事前確率まで分かっている前提ならば、これは最大事後確率推定(maximum a posteriori estimation; MAP推定)ともいえます。なんか最強っぽいですよね。
他に方法があるのでしょうか。スムージングという方法もあります。スムージングの中でも最も単純なのが ラプラススムージング とよばれる方法です。最尤推定の式の分子に1を加算して、分母に2を加算する方法です。
シミュレーションで確認
ではどちらがいいのでしょうか? 実際にシミュレーションして確認してみましょう。
以下のプログラムではまず真の確率 p を求めておき、そのpの確率に基づきn回コイン投げをして、その観測に基づき、最尤推定とスムージングによる推定をするようになっています。そして真の確率 p と答え合わせをします。最尤推定の方が近かった場合には+1を、あいこだった場合には+0.5をします。このゲームをt回繰り返し、最終的に最尤推定の勝率を表示します。
import random # --------------- 初期設定 t = 100000 # 確率あてゲーム回数 n = 3 # コイン投げ数 a = 0.01 # スムージングパラメータ(分子) b = 0.02 # スムージングパラメータ(分母) # --------------- 最終結果用変数初期化 win_sm = 0 # ラプラススムージングが勝った回数 sum_ml = 0.0 # 最尤推定の誤差の合計 sum_sm = 0.0 # スムージングの誤差の推定 # --------------- 確率あてゲーム(t回繰り返し) for i in range(t): p = random.random() # 真の表(おもて)の確率 # ------------ コイン投げによる施行 s = 0 # 表(おもて)の回数を初期化 for j in range(n): if p > random.random(): # 乱数が真の表の確率以下なら s += 1 # 表になる # ------------ 推定 ml = float(s)/n # 最尤推定 sm = (s+a)/(n+b) # スムージングによる推定 # ------------ 結果判定 diff_ml = (p-ml)**2 # 最尤推定の二乗誤差 diff_sm = (p-sm)**2 # スムージングの二乗誤差 if diff_sm < diff_ml: # ラプラススムージングの誤差のほうが小さければ、 win_sm += 1 # ラプラススムージングの勝ち++ elif diff_ml == diff_sm: # 同じならばあいこ win_sm += 0.5 # あいこのときは +0.5 sum_ml += diff_ml # 最尤推定の二乗誤差を集計する sum_sm += diff_sm # スムージングの二乗誤差を集計する # ------------- 表示 (デバッグ用) if t <= 50: print "s/n: %d/%d, p: %f, ml: %f, sm: %f" % (s, n, p, ml, sm) # ---------- 最終結果表示 win_sm_rate = float(win_sm)/t diff_ratio = sum_sm/sum_ml print "win sm rate: %f, sum_sm/sum_ml: %f" % (win_sm_rate, diff_ratio)
実行結果
s/n: 0/3, p: 0.046582, ml: 0.000000, sm: 0.200000 s/n: 2/3, p: 0.526964, ml: 0.666667, sm: 0.600000 s/n: 2/3, p: 0.420249, ml: 0.666667, sm: 0.600000 s/n: 2/3, p: 0.259805, ml: 0.666667, sm: 0.600000 s/n: 1/3, p: 0.387191, ml: 0.333333, sm: 0.400000 s/n: 1/3, p: 0.187301, ml: 0.333333, sm: 0.400000 s/n: 1/3, p: 0.530644, ml: 0.333333, sm: 0.400000 s/n: 1/3, p: 0.072210, ml: 0.333333, sm: 0.400000 s/n: 3/3, p: 0.968749, ml: 1.000000, sm: 0.800000 s/n: 0/3, p: 0.224703, ml: 0.000000, sm: 0.200000 s/n: 0/3, p: 0.053139, ml: 0.000000, sm: 0.200000 s/n: 0/3, p: 0.184094, ml: 0.000000, sm: 0.200000 s/n: 0/3, p: 0.108546, ml: 0.000000, sm: 0.200000 s/n: 2/3, p: 0.509613, ml: 0.666667, sm: 0.600000 s/n: 3/3, p: 0.284755, ml: 1.000000, sm: 0.800000 s/n: 0/3, p: 0.009353, ml: 0.000000, sm: 0.200000 s/n: 1/3, p: 0.500349, ml: 0.333333, sm: 0.400000 s/n: 1/3, p: 0.044538, ml: 0.333333, sm: 0.400000 s/n: 0/3, p: 0.080180, ml: 0.000000, sm: 0.200000 s/n: 0/3, p: 0.471813, ml: 0.000000, sm: 0.200000 win sm rate: 0.600000, sum_sm/sum_ml: 0.693820
最後の win sm rate: 0.600000 が最尤推定の勝率を表しています。ゲームの回数 t が20回というのはちょっと少ないので何度も実行するとこの勝率はかなり大きく変化します。そこでゲームの回数を思い切って t = 100000 くらいに設定してみましょう。
win sm rate: 0.597200, sum_sm/sum_ml: 0.595932
ラプラススムージングの勝率は6割程度もあるようですね。なんと、分子に1を足して、分母に2を足すというラプラススムージングの方が良いのです。
コイン投げを3回しか観測していないから悪いんじゃないか、という話もあります。ではコイン投げの回数nを20まで増やしてみましょう。
win sm rate: 0.529480, sum_sm/sum_ml: 0.911000
ラプラススムージングの勝率はかなり0.5に近づきましたが、まだ勝っていますね。では1000まで増やしてみましょう。(ちょっと時間がかかります)
win sm rate: 0.502880, sum_sm/sum_ml: 0.998269
ラプラススムージングの勝率はほとんど0.5に近づきましたが、まだ勝っていますね。実際1000回もチャンスをくれることというのもないかもしれませんが…。
分子に1を足して分母に2を足すだけで、予測が良くなってしまう、そんなお話でした。
なぜなの
最尤推定や最大事後確率推定では、最も尤度が高い確率を選んだにも関わらず、分子に1を足して分母に2を足すだけのラプラススムージングに負けてしまいました。この敗因は、最も高いところだけしか見ていないこと にあります。
次のグラフは、コイン投げで、表が1回、裏が4回のときのβ分布です。

最尤推定である、1/5 = 0.2 のところで最大となっていますが、面積的にはどうでしょうか? 0.2より大きい確率(右側)の方がずっと広いことがわかります。
尤度で重みを付けたpの期待値を求めてみましょう。
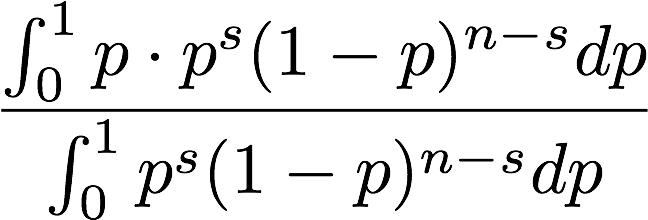
分母には重みである尤度の合計を持ってきています。分母と分子の二項係数は共にキャンセルされるので、消してあります。
これを maxima で解いてみましょう。
(%i1) beta_expand:true$
(%i2) integrate(p*p^s*(1-p)^(n-s),p,0,1)/integrate(p^s*(1-p)^(n-s),p,0,1);
Is s + 2 positive, negative or zero?
positive;
Is s - n - 1 positive, negative or zero?
negative;
WARNING: redefining MAXIMA::SIMP-UNIT-STEP in DEFUN
WARNING: redefining MAXIMA::SIMP-POCHHAMMER in DEFUN
Is s + 1 positive, negative or zero?
positive;
s + 1
(%o2) -----
n + 2
s や n に関して質問がありますが、なんと、ラプラススムージングが出てきました。ラプラススムージングは期待値だったのです。
まとめ
分子に1分母に2を足そう。
最も大きいところだけでなく、全体を見渡そう。
補足
事前確率について一様な場合について議論しました。一般的に事前知識に関して全く知識がない場合には無情報事前分布としてこのような一様分布を仮定します。
一方で、CTRって1%くらいだよね、とか、ナンパって全然成功しないよね、とか、今回の検証ケースではないにしても、他の情報にてある程度分かっている場合もあります。そのときには、共役事前分布を仮定して、経験ベイズ(エビデンス近似;第二種の最尤推定)といった方法で、ラプラススムージングにおける1と2に変わるパラメータ(超パラメータ;ハイパーパラメータ)を求めることを行います。二項分布に関して経験ベイズ法で超パラメータを抽出した話は下記の資料を御覧ください。
www.slideshare.netこのような技術を、fluct (SSP) ではアドネットワークを選択するバンディットアルゴリズムのパラメータに利用したり、fluct Direct Reach (DSP)では広告枠毎のCVRの予測のためのパラメータや、オーディエンスの属性推定などのパラメータとして利用しています。



